Abstract

Deep learning approaches in image processing predominantly resort to supervised learning. A majority of methods for image denoising are no exception to this rule and hence demand pairs of noisy and corresponding clean images. Only recently has there been the emergence of methods such as Noise2Void ^[3], where a deep neural network learns to denoise solely from noisy images. However, when clean images that do not directly correspond to any of the noisy images are actually available, there is room for improvement as these clean images contain useful information that fully unsupervised methods do not exploit. In this paper, we propose a method for image denoising in this setting. First, we use a flow-based generative model to learn a prior from clean images. We then use it to train a denoising network without the need for any clean targets. We demonstrate the efficacy of our method through extensive experiments and comparisons.

Some Background

Flow-based Generative Models

Simply put, a flow-based generative model ^[2] \((h)\) is a bijection between a pair of random variables. Typically, one of these random variables \((Z)\) is something for which the probability density function is known and tractable (e.g. Gaussian). While the other random variable \((X)\) is the one we are interested in modelling. In our case, the latter is a clean image. As in any deep neural network, \(h\) is a composition of many layers \(h_1, h_2, \dots, h_n\). Now, \begin{align} X = h(Z) &= h_n \circ h_{n-1} \circ \dots h_1 (Z)\\ \implies \log{f_X(x)} &= \log{f_Z(z)} - \sum_{i=1}^n \log{|J_{h_i}|}\\ \end{align} where \(J_{h_i}\) is the Jacobian of the \(i^{\text{th}}\) layer. The weights of the network \(h\) are trained by maximizing the above log-likelihood of \(X\). Note that you cannot use any old layer in \(h\); it has to be bijective and its Jacobian must be easy to compute. This rules out the most obvious choices such as convolution, pooling etc (at least not in their typical form). For some examples of layers that fit the bill, check out Dinh et al., Kingma et al. If you are interested in learning more theoretical details about flow-based generative models, see this excellent tutorial on flow-based generative models.

Core Idea

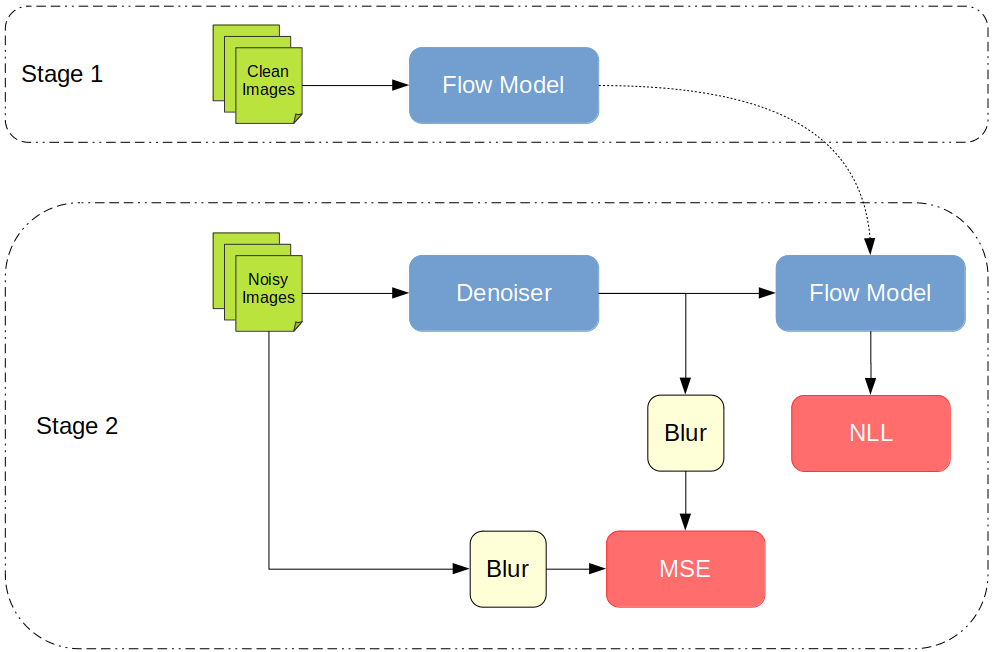
Our method proceeds in two stages:

Stage 1

In the first stage, we train a flow-based generative model on clean images. This will act as a prior \((f_C)\) for the denoiser that we train in the next stage.

Stage 2

Here, we train a ResNet to denoise images. Starting with the maximum a posteriori (MAP) estimate for the denoised image and a little bit of math, we arrive at the following objective, which we minimize: \begin{equation} (B(D) - B(N)) ^ 2 - \lambda \log {f_C(D)} \end{equation} where \(D\) is the denoised output image, \(N\) is the noisy input image, \(f_C\) is the prior from stage 1, \(\lambda \) is a hyperparameter that controls the relative weighting between the prior and the squared loss, and \(B\) is a blur kernel. To be precise, \(\lambda \) depends on the noise level \((\sigma)\). Bxut because we want our denoiser to work regardless of the noise strength, we blur the input and the output before computing the squared error. Intuitively speaking, this signals the network to reproduce the low-frequency information from the input (which is largely unaffected by noise), while using the prior to fill in the high-frequency details.

I encourage you to look at our paper for more details about the derivation and the training.

Results

Check out our paper for quantitative results.

Select References

1. Laurent Dinh, David Krueger, and Yoshua Bengio, “NICE: non-linear independent components estimation,” in 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Workshop Track Proceedings, Yoshua Bengio and Yann LeCun, Eds., 2015.
2. K. Dabov, A. Foi, V. Katkovnik, and K. Egiazarian, “Image denoising by sparse 3-d transform-domain collaborative filtering,” IEEE Transactions on Image Processing, vol. 16, no. 8, pp. 2080–2095, Aug 2007.
3. A. Krull, T. Buchholz, and F. Jug, “Noise2void - learning denoising from single noisy images,” in 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), June 2019, pp. 2124–2132.
4. Dmitry Ulyanov, Andrea Vedaldi, and Victor Lempitsky, “Deep image prior,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 9446–9454.